Podstawy analiz MES w praktyce

Symulacje numeryczne stanowią obecnie nieodzowną część procesu projektowania w wielu dziedzinach inżynierii. Dzięki rozwojowi środowisk do symulacji, ciągłemu wzrostowi wydajności komputerów i dostępności rozwiązań takich jak klastry obliczeniowe, obecnie analizy numeryczne dają prawie nieograniczone możliwości. Choć nadal często konieczne są uproszczenia ze względu na dostępną moc obliczeniową, zasymulować da się niemal dowolny obiekt i proces fizyczny. Dokładność takich analiz może być bardzo duża, ale jej osiągnięcie wymaga prawidłowego przygotowania modelu obliczeniowego.

W przypadku symulacji niezwykle łatwo jest o poważne błędy wynikające z wielu przyczyn. Obecnie powszechne są moduły do analiz w programach CAD, których prostota obsługi (często wystarczy dosłownie kilka kliknięć aby uruchomić analizę) bywa zwodnicza i przy nieznajomości zasad jakimi rządzą się symulacje można uzyskać wyniki fizycznie pozbawione sensu. Dlatego niezwykle ważne jest nie tylko zrozumienie podstaw wykorzystywanej metody numerycznej i modelowanego zagadnienia fizycznego, ale też dokładne weryfikowanie poprawności wyników, między innymi poprzez porównywanie ich z obliczeniami analitycznymi, gdy tylko jest to możliwe. Podstawy tego tematu zostały przedstawione w artykule Jak podejść do obliczeń wytrzymałościowych?

Podstawy teoretyczne i literatura

Najczęściej wykorzystywaną w inżynierii metodą numeryczną jest metoda elementów skończonych (MES) i to jej poświęcona będzie dalsza część artykułu. Pozostałe to głównie metoda objętości skończonych (powszechna w mechanice płynów – analizy CFD), różnic skończonych czy elementów brzegowych oraz tzw. metody bezsiatkowe – m.in. elementów dyskretnych (DEM) czy hydrodynamika wygładzonych cząstek (SPH). Mają one specyficzne zastosowania, ale to MES jest najbardziej uniwersalną metodą. Choć dokładna data powstania tej metody jest nieznana, jej początki sięgają lat 40. XX wieku a angielska nazwa, finite element method, została pierwszy raz użyta w artykule z 1960 roku. Znaczny wkład w rozwój MES miał inżynier i matematyk polskiego pochodzenia, Olgierd Zienkiewicz. Jego podręcznik „The Finite Element Method” był pierwszą książką w tym temacie i do dziś stanowi jedno z podstawowych opracowań dotyczących MES.

Metoda elementów skończonych jest w gruncie rzeczy przybliżoną metodą rozwiązywania równań różniczkowych. Równania tego typu opisują rozmaite zjawiska fizyczne, co pozwala wykorzystać MES do ich symulowania. Przykładowo, w mechanice konstrukcji rozwiązywane jest równanie równowagi ciała stałego. Równania różniczkowe są rozwiązywane na pewnych obszarach, z założeniem spełnienia określonych warunków na ich brzegach – tzw. zagadnienie brzegowe. W związku z tym, model komputerowy uzyskany np. z programu CAD musi zostać poddany dyskretyzacji. Polega ona na podzieleniu go na mniejsze fragmenty – elementy skończone o prostych kształtach (m.in. czworościany, sześciany), połączone w węzłach. Poszukiwane zmienne podstawowe (przemieszczenia w mechanice) są uzyskiwane w węzłach i ekstrapolowane na pozostałą część elementu przy pomocy funkcji kształtu. Ich rząd ma istotny wpływ na dokładność wyników uzyskiwanych przy pomocy danego elementu – ze względu na niego elementy można podzielić na liniowe (I rzędu) i kwadratowe (II rzędu). Te drugie mają dodatkowe węzły w środku krawędzi i znacznie lepiej odwzorowują krzywizny dyskretyzowanych modeli.

Warto przy tym podkreślić, iż programy do analiz MES nie rozwiązują bezpośrednio równań różniczkowych tylko macierzowe równanie, którego kluczową częścią jest macierz sztywności. Dla poszczególnych typów elementów wzór na lokalną macierz sztywności można uzyskać z równania różniczkowego przy pomocy metody ważonych residuów Galerkina (uzyskuje się tzw. postać słabą – w mechanice zasada prac przygotowanych) lub metody wariacyjnej Rayleigha-Ritza, opartej na minimalizacji funkcjonału (w mechanice minimum energii potencjalnej). Dla elementów prętowych można też skorzystać z metody bezpośredniej. Uzyskuje się w ten sposób tzw. sformułowanie elementu skończonego. Równanie rozwiązywane przez programy do analiz MES w liniowej statyce ma postać: [K]{u}={f}, gdzie [K] to macierz sztywności, {u} to wektor przemieszczeń zaś {f} to wektor sił węzłowych. Poszczególne etapy rozwiązywania zadania metodą elementów skończonych prowadzą do utworzenia tej globalnej macierzy (poprzez agregację macierzy lokalnych) i wektorów a następnie rozwiązania przytoczonego równania. Przemieszczenia są wyznaczane w węzłach, zaś odkształcenia i naprężenia są liczone na ich podstawie w tzw. punktach całkowania (Gaussa). W celu zrozumienia przebiegu obliczeń MES, najlepiej prześledzić przykłady przedstawiane w literaturze, na elementach sprężynowych, prętowych lub (rzadziej, ale wartościowo ze względu na dodatkowe aspekty jakie muszą zostać poruszone) 2D. W przypadku dynamiki, równanie wymaga rozbudowania do pełnej postaci, uwzględniającej macierze mas i tłumienia oraz wektory prędkości i przyspieszeń. W zagadnieniach nieliniowych dodatkowo pojawia się zależność macierzy sztywności od przemieszczeń i najczęściej wykorzystuje się metodą iteracyjno-przyrostową Newtona-Raphsona, polegającą na podziale obciążenia na przyrosty i wykonywaniu iteracji w ramach nich aż do uzyskania rozwiązania, czyli znalezienia równowagi poprzez porównywanie sił zewnętrznych i wewnętrznych i obliczanie różnicy między nimi nazywanej residuum aż osiągnie ona wartość niższą niż tolerancja w ustawieniach solvera. Ponadto zagadnienia dynamiczne można rozwiązywać na dwa sposoby – przy pomocy niejawnego (implicit) lub jawnego (explicit) całkowania równań ruchu po czasie.

Literatura do MES to głównie podręczniki opisujące podstawy teoretyczne tej metody. Za najlepszą z polskich książek tego typu uznawana jest „Metoda elementów skończonych w mechanice konstrukcji” G. Rakowskiego i Z. Kacprzyka. Jest ona również wykorzystywana przez osoby tworzące własne proste solvery MES. Inną godną polecenia pozycją tego typu jest „Zaawansowana metoda elementów skończonych w konstrukcjach nośnych” E. Rusińskiego, J. Czmochowskiego i T. Smolnickiego. Pozostałe warte uwagi książki poświęcone teorii MES to głównie podręczniki anglojęzyczne, autorów takich jak K.J. Bathe, R.D. Cook, K.H. Huebner, N. Ottosen, D.L. Logan, J. Fish i T. Belytschko, T.R. Chandrupatla i A.D. Belegundu, D.V. Hutton, P. Seshu, Y.W. Kwon czy S.S. Bhavikatti. Ciekawe przykłady prostych zadań można też znaleźć w książce U. Borkera. Dostępne są również książki omawiające pewne wybrane zagadnienia analiz numerycznych, jak np. „Non-linear Finite Element Analysis of Solids and Structures” autorstwa M.A. Crisfielda i innych. Szczególnie ciekawe mogą być podręczniki poświęcone aspektom praktycznym analiz MES. Jest ich niestety niewiele, ale warto zaopatrzyć się przede wszystkim w wydaną w 2020 r. książkę „Practical Finite Element Analysis for Mechanical Engineers” D. Madiera. Dość starą jak na tę dziedzinę (1998 r.), ale nadal w większości aktualną i zdecydowanie wartą uwagi pozycją jest „Building Better Products with Finite Element Analysis” V. Adamsa i A. Askenazi. Ciekawa jest również publikacja „Practical Finite Element Analysis” napisana przez N.S. Gokhale i innych. Autor ten w 2021 r. wydał jeszcze książkę „Practical Fatigue & Durability Analysis”. W tym samym roku wydana została też pozycja „Computational Structural Engineering. Automatic calculation of mechanical structures” C. Gianini. Ostatnim interesującym podręcznikiem tego typu jest „Practical Stress Analysis with Finite Elements” autorstwa B.J. Mac Donalda. Z literatury praktycznej przydatne mogą być również publikacje książkowe organizacji NAFEMS, obejmujące szeroki zakres tematów.

Oczywiście dostępne są książki poświęcone konkretnym programom do symulacji, ale zwykle stosunkowo trudno o dobrą pozycję tego typu. Niewątpliwie najcenniejszym źródłem informacji dla użytkownika danego środowiska MES jest jego dokumentacja, w której oprócz teorii i szczegółowych informacji dotyczących poszczególnych funkcjonalności, zawarte są zwykle również liczne przykłady. Wartościowe są też blogi poświęcone tematyce MES, zarówno te należące do producentów oprogramowania i ich partnerów jak i niezależne, tworzone np. przez firmy zajmujące się świadczeniem usług w dziedzinie analiz. Początkujący użytkownicy programów MES często sięgają po tutoriale na YouTube, ale należy do nich podchodzić ostrożnie, ponieważ mogą one zawierać poważne błędy.

Podstawowe funkcjonalności w programach do analiz MES

Środowiska do symulacji pozwalają na przejście całego procesu związanego z przeprowadzaniem symulacji (preprocessing – przygotowanie modelu, obliczenia i postprocessing – obróbka wyników) i wykonywanie analiz MES różnego typu. Podstawowe ich rodzaje to analizy statyczne, dynamiczne (kilka wariantów), wyboczeniowe i termiczne/termo-mechaniczne. Poza tym dostępne mogą być chociażby procedury optymalizacji, obliczeń z zakresu zmęczenia i mechaniki pękania, elektromagnetycznych czy akustycznych. Pozostałe typy symulacji, jak obliczeniowa mechanika płynów, zwykle wykonywane są przy pomocy innych metod numerycznych. Ponadto, wymienione zagadnienia fizyczne mogą być ze sobą łączone w tzw. analizach sprzężonych – np. naprężenia cieplne (mechanika i przepływ ciepła), przepływ płynów z przepływem ciepła czy mechanika z przepływem płynów (tzw. FSI – Fluid-Structure Interaction).

Programy do MES często wykorzystują podział analiz na kroki i pozwalają na łączenie różnych procedur obliczeniowych ze sobą (np. analiza modalna poprzedzona analizą statyczną). Istnieje również wiele typów modeli materiałowych wykorzystywanych w symulacjach. Pozwalają one opisać w uproszczony sposób zachowanie praktycznie dowolnego ośrodka ciągłego. Podstawowy model konstytutywny to liniowa sprężystość, ale bardzo często uwzględnia się też plastyczność (model biliniowy sprężysto-idealnie plastyczny, sprężysto-plastyczny ze wzmocnieniem lub wieloliniowy). Definicja klasycznej plastyczności z kryterium von Mises polega w przypadku modeli biliniowych na zdefiniowaniu granicy plastyczności i ew. modułu stycznego (tangent modulus) lub wprowadzeniu par naprężenie-odkształcenie plastyczne z krzywej rozciągania, co służy też definiowaniu modeli wieloliniowych. Stosowane są również modele hipersprężyste (głównie do gum i tkanek biologicznych), lepkosprężyste (głównie do tworzyw sztucznych), lepkoplastyczne (pełzanie i relaksacja naprężeń) oraz rzadziej spotykane, jak supersprężystość. Zwykle wykorzystuje się modele izotropowe, ale można również uwzględnić ortotropię/anizotropię (np. modelując drewno czy kompozyty). Często dostępne są kryteria zniszczenia materiału, które w połączeniu z opcją usuwania elementów pozwalają modelować np. przebijanie. Dane potrzebne do modeli materiałowych można uzyskać z testów fizycznych lub z publikacji naukowych, co jest bardzo częstym podejściem.

W programach do analiz MES dostępnych jest wiele typów elementów skończonych. Można dokonać ich podziału na różne sposoby, ale za podstawowy można uznać podział ze względu na ich geometrię:

• 1D – linie:

• belkowe – stosowane w przypadku konstrukcji, które można traktować jako prętowe, siatkę nakłada się na osie prętów,
• kratownicowe – elementy prętowe pracujące jedynie osiowo,
• ramowe – obecnie rzadko spotykane – wyparte przez uniwersalne elementy belkowe,

• 2D – powierzchnie:

• powłokowe – stosowane w przypadku konstrukcji cienkościennych, siatkę nakłada się wtedy na powierzchnię środkową powłoki,
• membranowe – podobnie jak elementy powłokowe, służą do modelowania konstrukcji cienkościennych, ale nie mają sztywności na zginanie,
• płytowe – przeznaczone tylko do zginania (nie przenoszą sił membranowych), obecnie rzadkie – wyparte przez elementy powłokowe,
• płaskiego stanu naprężeń – do analiz 2D (we współrzędnych XY) cienkich konstrukcji obciążonych w płaszczyźnie,
• płaskiego stanu odkształceń – do analiz 2D grubych konstrukcji obciążonych równomiernie na całej długości,
• osiowosymetryczne – do analiz 2D konstrukcji, które wraz z warunkami brzegowymi i obciążeniem wykazują symetrię osiową, osią symetrii zwykle musi być oś Y,

• 3D – bryły – najczęściej spotykane elementy ogólnego przeznaczenia.

Często dostępne są również takie specjalne typy elementów jak elementy sztywne (do modelowania części, które można w uproszczeniu potraktować jako idealnie sztywne) czy sprężyny i tłumiki. Poza tym, w wielu środowiskach dostępne są jeszcze bardziej specjalistyczne typy elementów skończonych przeznaczone m.in. do uproszczonej reprezentacji połączeń, uszczelek czy rur. Co ciekawe, istnieją również tzw. elementy nieskończone, służące do modelowania obszarów traktowanych jako nieograniczone.

W programach MES dostępnych jest wiele typów interakcji, takich jak kontakt, opisany w dalszej części artykułu, czy specjalne więzy łączące części w sposób sztywny lub z określoną podatnością oraz umożliwiające łączenie elementów różnych typów.

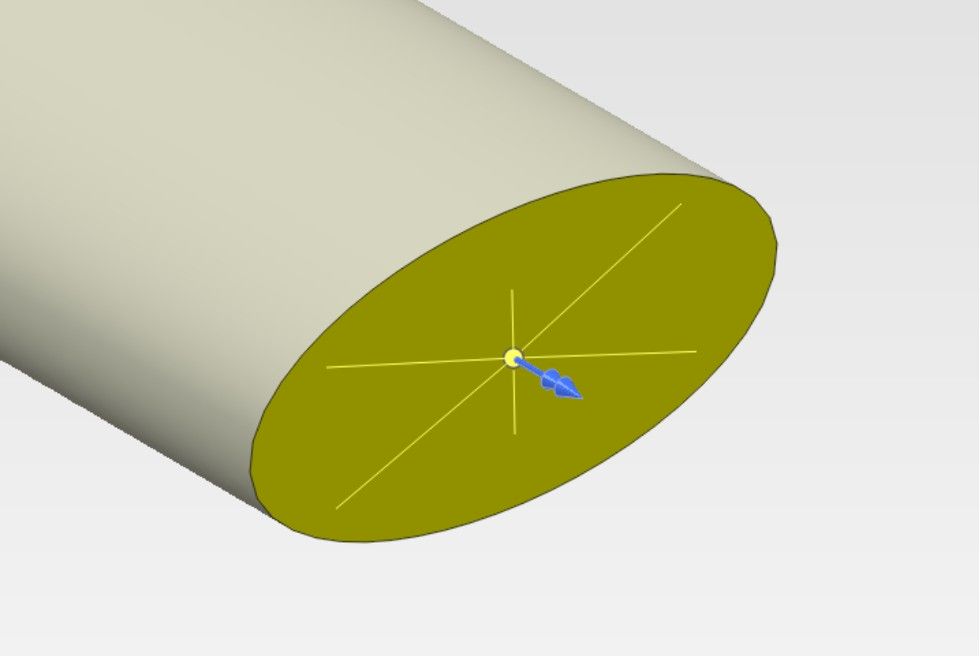
Warunki brzegowe w mechanice zwykle ograniczają się do blokowania przemieszczeń lub wymuszania ich niezerowych wartości w określonych kierunkach (stopniach swobody) w węzłach. Należy przy tym podkreślić, iż węzły elementów bryłowych, w przeciwieństwie do powłokowych czy belkowych, nie mają obrotowych stopni swobody. Wiążą się z tym m.in. utrudnienia w analizach skręcania, których wykonanie wymaga zwykle użycia specjalnych typów interakcji łączących ruch węzłów z ruchem punktu referencyjnego, do którego można przyłożyć moment obrotowy lub warunek brzegowy działający na obrotowe stopnie swobody. Taki więz jest symbolicznie przedstawiony na rysunku poniżej.

W analizach dynamicznych wykorzystywane są również analogiczne warunki brzegowe nakładane na prędkości i przyspieszenia. Z kolei w analizach termicznych warunkiem brzegowym jest zadana temperatura. Dla symulacji uwzględniających czas istotne są też warunki początkowe – np. temperatura początkowa lub prędkość początkowa.

Obciążenia dostępne w programach MES to przede wszystkim siły skupione przykładane do węzłów, ale też różnego rodzaju obciążenia rozłożone. Mogą one być przykładane na powierzchnie (ciśnienie równomiernie rozłożone lub zmienne, obciążenie styczne do powierzchni – w metodzie elementów skończonych przekształcane na siły węzłowe) lub stanowić siły masowe, takie jak obciążenie grawitacyjne czy odśrodkowe. Często dostępne są specjalne, predefiniowane typy obciążeń, jak napięcie wstępne śruby. W analizach termicznych obciążenia stanowią strumienie cieplne – skupione, powierzchniowe, objętościowe oraz konwekcja i promieniowanie cieplne. Zarówno obciążenia jak i warunki brzegowe często mogą być definiowane w lokalnych układach współrzędnych, ze zmiennością przestrzenną lub w czasie (niekoniecznie fizycznym – analizy nieliniowe statyczne bez zależności właściwości materiału od szybkości odkształceń wykorzystują czas tylko jako zmienną do inkrementacji obciążeń).

Programy do analiz MES często oferują również pewne specjalne techniki modelowania, takie jak submodeling, który polega na przenoszeniu wyników z modelu pełnej konstrukcji na model ograniczony do jej fragmentu i mający bardziej zagęszczoną siatkę a czasami również uwzględniający dodatkowe szczegóły. Inną zbliżoną techniką jest tworzenie i wykorzystywanie substruktur (w literaturze nazywanych superelementami). Metoda ta pozwala stworzyć z danego fragmentu konstrukcji element skończony, który następnie wykorzystywany jest w analizach gdzie ten fragment konstrukcji się pojawia (zwykle wielokrotnie). Dzięki temu obliczenia są szybsze, ponieważ substruktura ma już wyznaczoną m.in. macierz sztywności czy macierz mas, ale może podlegać tylko liniowo-sprężystym deformacjom. Inne specjalne techniki dotyczą chociażby kontynuowania analiz – istnieją sposoby „doliczania” kolejnych etapów symulacji mając już ukończone poprzednie etapy.

Zakres danych jakie można uzyskać z symulacji numerycznych jest bardzo szeroki. Podstawowe wyniki w przypadku mechaniki konstrukcji to mapy konturowe naprężeń (zredukowanych von Mises, składowych tensora czy głównych), odkształceń, przemieszczeń i reakcji. Często dostępne są narzędzia pozwalające na sprawdzanie wartości w wybranym węźle/elemencie, tworzenie przekrojów, wykonywanie wykresów XY, przekształcanie do lokalnych układów współrzędnych, wizualizacje grubości elementów 2D itd. Ważne jest zrozumienie tego jak dana zmienna jest liczona i do czego można ją stosować. Przykładowo, klasyczne naprężenia von Mises porównywane z granicą plastyczności lub wytrzymałością materiału są przeznaczone przede wszystkim do oceny materiałów ciągliwych. Inne materiały mogą wymagać użycia odmiennych kryteriów zniszczenia i sprawdzania naprężeń głównych bądź odkształceń.

Siatki elementów skończonych

Najczęstsze przyczyny błędów w modelowaniu MES to niewystarczająco gęsta i złej jakości siatka elementów skończonych oraz nieodpowiednie warunki brzegowe, które nieprawidłowo odwzorowują rzeczywisty sposób podparcia konstrukcji. Ten drugi problem zostanie omówiony w kolejnej sekcji artykułu. Przygotowanie siatki do analiz MES wymaga szczególnej uwagi ze strony inżyniera. Istotny jest dobór rodzaju elementów (typ, I/II rząd, pełne/zredukowane całkowanie itd.) do danego przypadku oraz uzyskanie dobrej jakości siatki. Z reguły zaleca się tworzenie siatek z elementów prostopadłościennych (hexahedral), co jednak nie zawsze jest możliwe ze względu na geometrię modelu. W przypadku bardzo skomplikowanych kształtów konieczne może być wykorzystanie elementów czworościennych (tetrahedral). Potrzeba ich więcej by uzyskać odpowiednią dokładność, ale nie są to elementy, których należy za wszelką cenę unikać.

Mniej zaawansowane programy, zwłaszcza moduły MES w środowiskach CAD, często oferują tylko elementy czworościenne. Przyjmuje się, że w obliczeniach uwzględniających zginanie siatka powinna mieć co najmniej 3-4 elementy po grubości. W przypadku cienkich konstrukcji, takich jak blachy, wymagałoby to korzystania z bardzo gęstych siatek i dlatego do modelowania takich konstrukcji wykorzystuje się elementy powłokowe, w których grubość jest definiowana jako charakterystyka elementu. Analogicznie dla smukłych konstrukcji wykorzystuje się elementy prętowe, głównie belkowe, w przypadku których parametry przekroju są charakterystyką elementu. Należy również pamiętać o zjawisku tzw. hourglassingu, które powoduje błędne deformacje gdy do modelowania zginania wykorzystuje się zbyt mało (po grubości) elementów liniowych ze zredukowanym całkowaniem (tylko 1 punkt całkowania). Widoczne jest to jako charakterystyczne pofalowanie elementów. Z kolei w przypadku elementów liniowych z pełnym całkowaniem może wystąpić tzw. shear locking, czyli przesztywnione wyniki przy zginaniu. Stąd zaleca się użycie elementów kwadratowych (II rzędu) do modelowania tego typu deformacji. Po wizualnej ocenie siatki zaleca się sprawdzić w programie parametry charakteryzujące jej jakość, takie jak współczynnik kształtu (aspect ratio), skośność (skewness) czy Jacobian. Na tym jednak nie kończy się weryfikacja siatki. Po uzyskaniu pierwszych wyników, dobrą praktyką jest zagęszczenie siatki (najlepiej lokalne – w miejscach koncentracji naprężeń, jak to pokazano na rysunku poniżej) i ponowne przeprowadzenie analizy a następnie powtórzenie tej procedury. Sprawdzając wyniki w kolejnych iteracjach należy zwracać uwagę na zmiany maksymalnych przemieszczeń i naprężeń. Powinny one się zbiegać do stałej wartości. Przy niewielkiej (ok. 5%) różnicy można uznać, że dokładność jest wystarczająca i zakończyć takie studium gęstości siatki. Jeśli mimo zagęszczania siatki naprężenia maksymalne w miejscu ich koncentracji nie przestają rosnąć to możemy mieć do czynienia ze zjawiskiem osobliwości naprężeń (stress singularity), które zwykle wynika z zadania siły lub warunku brzegowego na pojedynczy węzeł w modelu 3D, kontaktu krawędziowego lub występowania ostrego narożnika. Istnieje kilka podejść w takich przypadkach:

• zadawanie obciążeń i warunków brzegowych na małe obszary zamiast pojedynczych punktów,
• dodawanie zaokrągleń do ostrych krawędzi,
• uwzględnianie plastyczności w modelu materiałowym,
• ignorowanie tego zjawiska i odczytywanie naprężeń z dala od obszaru jego występowania, jeśli to możliwe w danym przypadku.

Warunki brzegowe

Kwestia warunków brzegowych również jest niezwykle istotna w MES. Powinny one jak najdokładniej odpowiadać rzeczywistym podparciom konstrukcji. Częstym błędem jest przesztywnianie modeli poprzez nadmierne używanie warunku brzegowego pełnego utwierdzenia (blokada wszystkich stopni swobody). Przykładowo, konstrukcja stojąca swobodnie na podłożu (nie przytwierdzona do niego) nie powinna mieć zablokowanych wszystkich stopni swobody u podstawy. Jednak bardzo często problem przy doborze warunków brzegowych stanowi fakt, iż w analizach statycznych niedopuszczalne są tzw. ruchy ciała sztywnego – model nie może być mechanizmem i musi mieć minimalne więzy, takie by nie mógł swobodnie przemieszczać się ani obracać w żadnym kierunku w przestrzeni.

Oto kilka przykładowych sytuacji dla modeli bryłowych:

• model, w którym jeden wierzchołek ma zablokowane wszystkie stopnie swobody (a więc 3 translacje) nadal może obracać się swobodnie wokół tego wierzchołka,
• model z utwierdzoną jedną krawędzią może się wokół niej obracać,
• model z utwierdzonymi 3 wierzchołkami nie leżącymi na jednej linii jest stabilny,
• model z 2 prostopadłymi do siebie ścianami unieruchomionymi w kierunkach do nich normalnych może się przesuwać w trzecim kierunku,
• model z 3 prostopadłymi do siebie ścianami unieruchomionymi w kierunkach do nich normalnych jest stabilny.

W zapobieganiu ruchom sztywnym istotną rolę odgrywa również kontakt między częściami złożenia, wymuszone przemieszczenia czy warunki symetrii. W przypadku problemów z uniknięciem ruchów sztywnych można też stosować specjalne techniki oferowane przez niektóre programy do analiz MES – obciążenie bezwładnościowe (inertia relief), miękkie sprężyny (soft springs), dyskretne tłumiki/sprężyny czy stabilizację/tłumienie w analizie. Niektóre programy pozwalają na analizy statyczne modeli z równoważącym się obciążeniem (np. zbiornik z równomiernym ciśnieniem wewnętrznym, pręt skręcany momentami o przeciwnych zwrotach na 2 końcach), ale należy zachować ostrożność w takich przypadkach i lepiej uwzględniać warunki brzegowe w miarę możliwości.

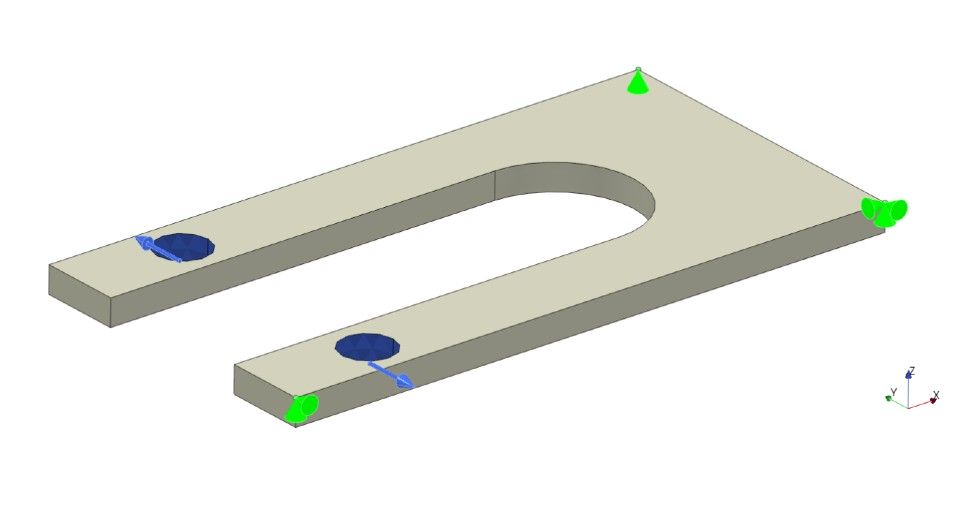
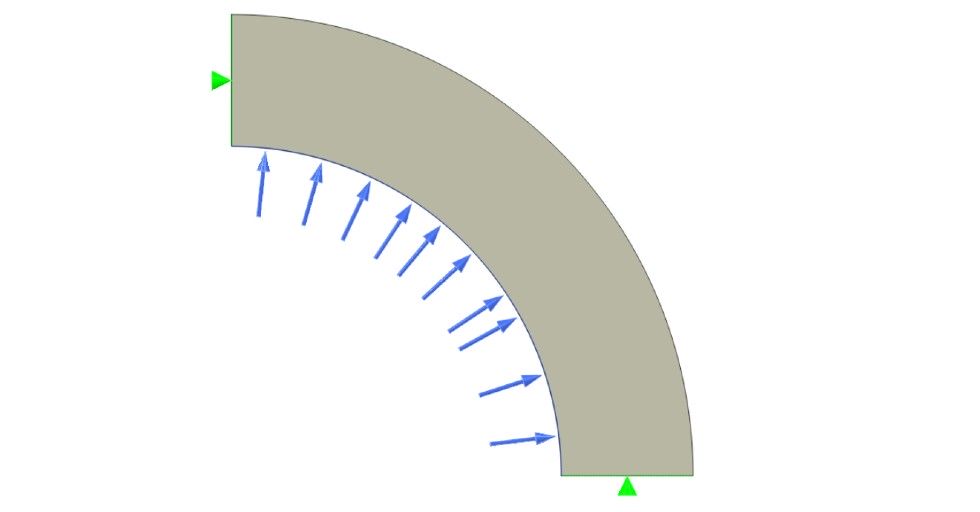
Dobierając warunki brzegowe do modelu z równoważącym się obciążeniem można wykorzystać specjalną metodę 3-2-1 zalecaną przez NAFEMS i polegającą na odpowiednim dobraniu i podparciu 3 węzłów:

• pierwszy ma zablokowane wszystkie 3 przemieszczenia (co eliminuje translacyjne ruchy sztywne),
• drugi ma zablokowane 2 przemieszczenia – w dwóch kierunkach normalnych do wyobrażalnej linii łączącej pierwszy i drugi węzeł (co eliminuje dwa rotacyjne ruchy sztywne, ale pozostawia obrót wokół tej linii),
• trzeci ma zablokowane 1 przemieszczenie – w kierunku normalnym do płaszczyzny, w której leżą wszystkie 3 węzły (co eliminuje ostatni rotacyjny ruch sztywny).

Aby sprawdzić czy warunki brzegowe w tej metodzie zostały odpowiednio ustawione, można przeprowadzić analizę uwzględniającą rozszerzalność cieplną i upewnić się, że możliwe jest swobodne rozszerzanie się lub kurczenie modelu bez powstawania znaczących reakcji w podporach. W analizach 2D również można stosować metodę 3-2-1 – wtedy wymagane są tylko 2 podparcia. Także występowanie w modelu symetrii redukuje liczbę potrzebnych węzłów. Metoda ta nie nadaje się jednak do analiz z nieliniowością geometryczną. Przykład wykorzystania tego podejścia został zilustrowany poniżej. Zielone symbole dotyczą warunków brzegowych (translacje w poszczególnych osiach) a niebieskie obciążenia. Wszystkie rysunki w tym artykule zostały przygotowane przy pomocy darmowego programu PrePoMax opisanego w publikacji PrePoMax. Najlepszy darmowy program do analiz MES? [O programie + TEST].

Bardzo dobrym sposobem na sprawdzenie czy w modelu nie występują ruchy sztywne (weryfikacja poprawności warunków brzegowych i połączeń między częściami) jest przeprowadzenie analizy drgań własnych – ruchy te będą widoczne w pierwszych postaciach drgań, z częstościami bliskimi 0 Hz.

Kontakt

Jednym z najtrudniejszych i najbardziej problematycznych zagadnień w analizach MES jest kontakt. Należy go rozumieć jako styk powierzchni dwóch ciał stałych z przekazywaniem sił w kierunku normalnym i (jeśli uwzględnione jest tarcie) stycznym. Kontakt jest zjawiskiem silnie nieliniowym, ponieważ jego stan może się zmieniać w trakcie analizy – części mogą być początkowo rozdzielone a następnie wejść ze sobą w kontakt, przesuwać się po sobie, dociskać czy rozdzielać. Często dla uproszczenia korzysta się z tzw. kontaktu wiązanego (tied/bonded contact) lub odpowiadających mu więzów, które nie pozwalają na wzajemne przesuwanie się i rozdzielanie powierzchni a więc symulują trwałe połączenie części. Są one stosowane wtedy, gdy siatki części wchodzących w skład złożenia nie są ciągłe (ich ciągłość można zapewnić przy pomocy specjalnych narzędzi do scalania części i siatek w programach CAD i MES). Należy też pamiętać o tym, że wiązania nadawane przy tworzeniu złożeń w programach CAD nie mają wpływu na analizę.

Klasyczny algorytm kontaktu stosowany w MES jest oparty o koncepcje powierzchni master i slave tworzących parę kontaktową. Powierzchnia master jest nadrzędna i jej węzły mogą w niewielkim stopniu przenikać powierzchnię slave a w drugą stronę nie jest to możliwe. Przypisując powierzchnię należy pamiętać o kilku standardowych zasadach. Powierzchnią master powinna być powierzchnia należąca do części idealnie sztywnej lub sztywniejszej od drugiego komponentu biorącego udział w kontakcie, o rzadszej siatce, większa i mniej zakrzywiona. Spełnienie tych kryteriów (zwłaszcza w kwestii gęstości siatki) pozwala uniknąć wielu problemów z kontaktem. Co ciekawe, często wspierany jest tzw. self contact, czyli kontakt między różnymi obszarami tej samej powierzchni należącej do ciała podlegającego znacznym deformacjom.

Programy do MES mają obecnie bardzo rozbudowane implementacje kontaktu. Dostępne są w nich różne metody dyskretyzacji, wymuszania więzów czy śledzenia kontaktu. Wśród sposobów wymuszania więzów kontaktowych najczęściej wyróżnia się metodę penalty (funkcja kary), która dopuszcza pewne penetracje, ale lepiej się zbiega i mnożników Lagrange’a, która jest dokładniejsza, ale spowalnia obliczenia i utrudnia osiągnięcie zbieżności. Można również definiować różne właściwości kontaktu – dla kierunku normalnego zależności ciśnienia od penetracji a dla kierunku stycznego modele tarcia.

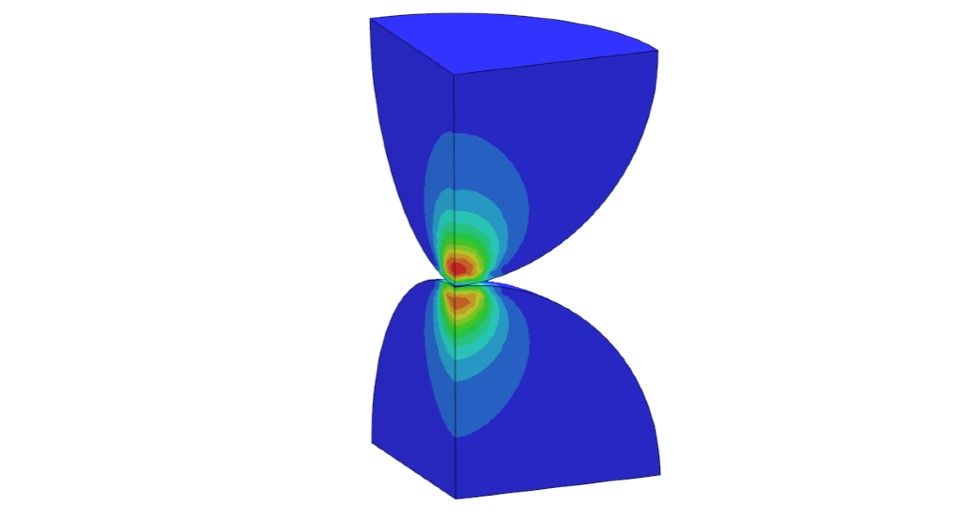
Trudności przy modelowaniu kontaktu wynikają m.in. z występujących w analizie ruchów sztywnych, których nie eliminują w pełni warunki brzegowe i konieczne jest poleganie na kontakcie. Zwłaszcza na początku analizy może on nie być prawidłowo ustanowiony i konieczne jest stosowanie pewnych obejść by uzyskać zbieżność analizy. Najczęściej sprowadza się to do:

• zastosowania wymuszonego przemieszczenia zamiast siły – ogólnie zalecane w analizach nieliniowych,
• unikania początkowych przerw między częściami – lepsze mogą być nawet niewielkie przenikania, z których program wycofa się bez odkształceń (lub z odkształceniami jeśli modelowane jest połączenie wciskowe),
• stosowania stabilizacji kontaktu/tłumienia jeśli dany program na to pozwala,
• przeprowadzania analizy dynamicznej quasi-statycznej,
• użycia dodatkowego etapu analizy, w którym kontakt jest najpierw osiągany a dopiero w kolejnym kroku zadawane jest właściwe obciążenie,
• użycia elementów typu miękkie sprężyny lub tłumiki do zapobiegania ruchom sztywnym, jak opisano w części dotyczącej warunków brzegowych.

Podstawowe typy analiz MES i ich cechy

Najczęściej spotykanym typem analiz MES są analizy statyczne liniowe. Zakładają one liniową odpowiedź konstrukcji (materiał liniowo-sprężysty, małe odkształcenia, brak zmieniającego się kontaktu) i statyczny charakter obciążenia oraz odpowiedzi. Przyjmuje się, że obciążenie jest zadawane tak wolno, że nie powoduje żadnych efektów dynamicznych. Jednak analizy tego typu mogą uwzględniać ustalone obciążenia bezwładnościowe, takie jak przyspieszenie grawitacyjne czy siły odśrodkowe (konieczne zdefiniowanie gęstości materiału) a nawet pozwalają modelować stałą prędkość obrotową. Analizy te cechuje skalowalność, a więc np. dwukrotne zwiększenie obciążenia spowoduje dwukrotny wzrost przemieszczeń.

Kolejnym powszechnym typem symulacji są analizy statyczne nieliniowe. Pozwalają one uwzględnić wszystkie 3 typy nieliniowości w MES:

• materiałową – nieliniowa zależność naprężeń od odkształceń,
• geometryczną – zmiana sztywności przy dużych deformacjach, wyboczeniu, obciążeniu wstępnym (aby ta forma nieliniowości została uwzględniona w analizie, zwykle należy włączyć odpowiednią opcję w ustawieniach symulacji),
• brzegową – zmieniający się kontakt czy tzw. siły podążające (follower forces).

Jak to zostało wspomniane w części artykułu dotyczącej teorii MES, tego typu analizy są zwykle liczone metodą Newtona-Raphsona. Uzyskanie zbieżności może być w przypadku tej metody trudne jeśli występują silne niestabilności. Stąd, do analiz nieliniowych wyboczenia często wykorzystuje się specjalną metodę długości łuku (Riksa) lub sięga po sztuczne tłumienie bądź analizy dynamiczne. Wyboczenie liniowe jest zaś liczone przy pomocy osobnych procedur, opartych o zagadnienie własne. Z tych symulacji uzyskuje się współczynniki obciążenia krytycznego, które należy pomnożyć przez wartość zadanego obciążenia (dlatego często zadaje się jednostkowe obciążenie w tych analizach) i postaci wyboczenia, które po odpowiednim przeskalowaniu można wykorzystać jako imperfekcje geometryczne w symulacjach wyboczenia nieliniowego. Należy przy tym pamiętać, iż analizy wyboczenia liniowego nie pozwalają uzyskać rzeczywistych wartości przemieszczeń i naprężeń, ponieważ wielkości te podlegają normalizacji.

Analogiczny podział na analizy liniowe i nieliniowe występuje w przypadku dynamiki. Podstawową procedurą obliczeniową dynamiki liniowej jest analiza częstości drgań własnych, będąca rozwiązaniem zagadnienia własnego, podobnie jak w przypadku wyboczenia liniowego. Uzyskuje się częstości drgań własnych (istotne m.in. dla uniknięcia zjawiska rezonansu – wymuszenia o takich częstotliwościach mogą powodować znaczący wzrost amplitudy drgań) i odpowiadające im postaci drgań. Tu również przemieszczenia i naprężenia nie są rzeczywistymi wielkościami. Ponadto w tego typu analizach nie definiuje się obciążeń. Postaci drgań często są wykorzystywane przez inne procedury z grupy liniowej dynamiki, oparte o metodę superpozycji modalnej.

Można tu wyróżnić analizy:

• drgań ustalonych (steady-state, harmonic) – obciążenie harmoniczne, odpowiedź w dziedzinie częstotliwości,
• drgań nieustalonych (transient) – obciążenie i odpowiedź w dziedzinie czasu,
• drgań losowych (random) – obciążenie definiowane w postaci krzywej PSD (power spectral density – gęstość widmowa mocy), odpowiedź w dziedzinie częstotliwości,
• spektrum odpowiedzi (response spectrum) – szacowanie szczytowej odpowiedzi konstrukcji w dziedzinie częstotliwości na ruch podłoża zdefiniowany jako tzw. spektrum odpowiedzi, stosowane często w analizach budowli pod wpływem trzęsień ziemi.

Analizy dynamiczne nieliniowe są z kolei przeprowadzane przy pomocy bezpośredniego całkowania równań ruchu, wspomnianymi już wcześniej metodami implicit lub explicit. Symulacje typu explicit dynamics wykorzystuje się głównie do tzw. szybkiej dynamiki (uderzenia, upadki, crash testy, wybuchy itp.) oraz analiz quasi-statycznych zagadnień silnie nieliniowych, takich jak procesy obróbki plastycznej. W analizach explicit nie ma iteracji i problemów ze zbieżnością, ale pojawia się problem warunkowej stabilności i związana z nim koncepcja stabilnego przyrostu czasowego – nawet pojedyncze małe elementy bardzo wydłużają czas potrzebny na ukończenie analizy i konieczne może być stosowanie obejść takich jak sztuczne przyspieszanie symulowanego procesu quasi-statycznego (z zachowaniem odpowiednio niskiej energii kinetycznej) czy stosowanie tzw. skalowania masy (na stabilny przyrost czasowy wpływa też gęstość materiału).

Uwagi końcowe

Warto jeszcze omówić kilka dobrych praktyk związanych z wykonywaniem analiz MES. Po pierwsze, modele z programów CAD zwykle wymagają uproszczeń pod kątem symulacji. Należy eliminować wszelkie detale, których wpływ na odpowiedź konstrukcji nie jest znaczący i które nie są obiektem zainteresowania w analizie. Dotyczy to przede wszystkim wszelkich wygrawerowanych napisów/symboli czy innych elementów bardzo małych w stosunku do całego modelu (np. drobne zaokrąglenia), ale często również spoin (te zwykle są pomijane w analizach lub liczone osobno pod kątem zmęczenia) i śrub (choć istnieją różne sposoby modelowania tego typu połączeń). W przypadku złożeń nie zawsze trzeba uwzględniać w symulacji wszystkie części, niektóre z nich można zastępować odpowiednimi więzami i np. traktować jako idealnie sztywne lub zastąpić tzw. odległym obciążeniem/masą.

Gdy model jest już pozbawiony zbędnych detali, należy jeszcze zastanowić się nad przygotowaniem jego uproszczonej reprezentacji skracającej czas trwania analiz MES. Dotyczy to przede wszystkim często spotykanej symetrii. Jeśli model, warunki brzegowe, obciążenia i odpowiedź spełniają warunki jednego z typów symetrii to zaleca się skorzystanie z niego:

• symetria planarna – warunki brzegowe blokujące przemieszczenia w kierunku normalnym do powierzchni (dla elementów z obrotowymi stopniami swobody w węzłach dodatkowo blokada obrotów innych niż wokół osi, w której zablokowane są przesunięcia), pozwala zamodelować 1/2, 1/4 a nawet 1/8 konstrukcji w zależności od tego ile ma ona płaszczyzn symetrii, często korzysta się z tego typu uproszczeń np. w przypadku zbiorników,
• symetria osiowa – elementy osiowosymetryczne wspomniane wcześniej,
• symetria cykliczna – specjalne więzy, dostępne w wielu programach, pozwalają na modelowanie segmentów konstrukcji takich jak wirniki, możliwy jest obrót wokół osi symetrii.

Istnieje jeszcze antysymetria, ale jest ona dość rzadko wykorzystywana. Innym uproszczeniem, na które niekiedy można sobie pozwolić w symulacji jest potraktowanie konstrukcji jako dwuwymiarowej i użycie wspomnianych już elementów płaskiego stanu naprężeń bądź płaskiego stanu odkształceń. Również analizy termiczne czy przepływowe pozwalają na takie uproszczenia. Należy też zawsze zastanowić się czy dana konstrukcja nie może być zamodelowana przy pomocy elementów powłokowych lub belkowych jeśli jest cienkościenna lub smukła.

Dobre praktyki dotyczące obróbki wyników to przede wszystkim dokładne ich sprawdzanie pod różnymi względami – od pierwszych oględzin i oceny czy podstawowe wyniki, takie jak naprężenia, przemieszczenia oraz przeskalowana i nieprzeskalowana deformacja (pomocne mogą być animacje), mają sens w danym przypadku po bardziej dokładną weryfikację. Obejmuje ona m.in. sprawdzenie równowagi przyłożonych obciążeń i sumy uzyskanych reakcji w poszczególnych kierunkach, sprawdzenie globalnych energii modelu, ciągłości pól naprężeń (z wyłączonym ich uśrednianiem), zwrócenie uwagi na wszelkie ostrzeżenia generowane przez program, sprawdzenie poprawności działania kontaktu i innych więzów, dokładne przyjrzenie się wszelkim koncentracjom naprężeń itd. Jeśli to tylko możliwe, ważne jest porównanie wyników z obliczeniami analitycznymi, co zostało wspomniane na początku artykułu.

Podsumowując, analizy MES należy wykonywać z rozwagą i zrozumieniem danego zagadnienia. Uzyskane wyniki trzeba dokładnie weryfikować by uniknąć poważnych błędów. W miarę możliwości warto sprawdzić różne techniki modelowania określonego problemu. Istotną zaletą symulacji jest praktyczny brak kosztu (innego niż czas, energia elektryczna itp.) samego ich wykonywania, więc mając wątpliwości co do sposobu działania programu w jakimś przypadku, warto samemu to sprawdzić robiąc jak najprostsze testy. Przykładowo, częstą wątpliwością wśród początkujących użytkowników programów do symulacji jest to czy zmiana modułu Younga w prostej liniowej analizie statycznej z jednym materiałem wpływa na naprężenia czy tylko na deformacje. Aby uzyskać odpowiedź na to pytanie wystarczy przygotować prosty model belki zginanej i sprawdzić jak zmienią się wyniki po zmianie modułu Younga. Zachęcam zainteresowanych czytelników do przetestowania tego samemu. Innym przykładem często wykonywanych przez użytkowników testów jest sprawdzenie działania różnych typów obciążeń – tego jak są rozkładane na wskazanych powierzchniach. Jest to o tyle istotne, że niektóre programy mają obciążenia w formie sił skupionych, które można zadawać na całe powierzchnie, ale powodują one, że każdy węzeł należący do powierzchni jest obciążony podaną wartością siły co powoduje znaczne (i na szczęście łatwe do zauważenia) przekłamania w wynikach jeśli intencją użytkownika jest obciążenie danej powierzchni równomiernie wprowadzoną wartością siły (tak, że każdy węzeł jest obciążony tylko jej odpowiednią częścią). Najlepiej jeśli modele używane w tego typu testach nadają się też do porównania z obliczeniami analitycznymi.

Kolejną istotną kwestią jest fakt, iż wiele profesjonalnych programów do analiz MES nie obsługuje jednostek i po stronie użytkownika jest zadbanie o to, by wprowadzać wartości w odpowiednim układzie jednostek (zgodnym dla całego modelu). Łatwo o błędy tym spowodowane, ale tu również dokładne sprawdzanie wyników pozwala uniknąć problemów.

Na koniec warto wspomnieć o ogólnym podejściu zalecanym w przypadku trudności z przeprowadzaniem analiz MES, takich jak problemy ze zbieżnością, nieprawidłowe wyniki czy podejrzenia błędów w programie. Model należy stopniowo upraszczać, usuwając lub wygaszając (jest to możliwe w wielu programach) jego poszczególne cechy aż błąd przestanie występować. Pozwala to zidentyfikować źródło problemów. W pierwszej kolejności warto zwrócić uwagę na wszelkie niestandardowe modele materiałowe, typy elementów czy więzów. Jeśli problemy dotyczą kontaktu, można redukować jego użycie w modelu łącząc wybrane części trwale lub przytrzymując je warunkami brzegowymi. Do  takich testów przydaje się też możliwość ustawienia wybranych części jako idealnie sztywnych. Jeśli zaś stosuje się zaawansowane modele materiałowe i pojawiają się wątpliwości co do poprawności ich działania w danym przypadku to warto przeprowadzić testy na pojedynczych elementach poddanych różnym typom i zakresom obciążeń.

W artykule przedstawione zostały jedynie podstawy praktycznych zagadnień analiz MES, ponieważ temat ten jest niezwykle obszerny i złożony. W połączeniu z innymi źródłami informacji wskazanymi na początku może jednak stanowić przydatne źródło informacji dla inżynierów zainteresowanych symulacjami numerycznymi. Pozostaje jedynie zachęcić czytelników do zgłębiania tej tematyki i przede wszystkim samodzielnego wykonywania jak największej liczby testowych analiz oraz dokładnego przyglądania się ich wynikom, co jest najlepszym sposobem na zaznajomienie się z oprogramowaniem i symulacjami w ogóle.