Jak podejść do obliczeń wytrzymałościowych?

Niezwykle istotną częścią procesu projektowania jest dokonywanie obliczeń, mających na celu sprawdzenie wytrzymałości i sztywności produktu w danych warunkach pracy. Obecnie wykorzystuje się w tym celu analizy numeryczne oparte na metodzie elementów skończonych (MES). Środowiska do tych symulacji są dziś powszechnie dostępne, również jako moduły w praktycznie wszystkich wiodących programach CAD 3D. Z tego powodu, klasyczne obliczenia wytrzymałościowe wykonywane metodami analitycznymi w wielu przypadkach schodzą na dalszy plan lub są całkowicie pomijane. Należy jednak pamiętać o tym, iż w symulacjach numerycznych łatwo o poważne błędy mogące wynikać z wielu przyczyn (niepoprawne dane wejściowe, złe podejście do tworzenia modelu komputerowego, nieznajomość programu, rzadziej błąd w samym programie). Z tego względu zaleca się nie tylko dokładne sprawdzanie wyników symulacji na różne sposoby, ale też ich weryfikację za pomocą obliczeń analitycznych gdy tylko jest to możliwe. Niestety w wielu przypadkach nie da się tego zrobić ze względu na zbyt skomplikowaną geometrię lub fizykę zagadnienia. Często jednak możliwe jest uzyskanie analitycznie przybliżonej wartości czy chociaż rzędu wielkości jakiego powinniśmy się spodziewać w wynikach symulacji. Są też przypadki, które łatwo można zweryfikować analitycznie a nawet benchmarki, gdzie znane jest dokładne rozwiązanie i ocenia się zgodność wyników analizy w danym programie z tymi znanymi wartościami.

Ogólne podejście do obliczeń wytrzymałościowych

Studia na wydziałach mechanicznych i budowlanych zawsze obejmują wytrzymałość materiałów w swoim programie. Po takim kursie, każdy inżynier powinien znać definicje naprężeń, odkształceń itp. oraz umieć rozwiązywać podstawowe przypadki wytrzymałościowe, takie jak belki zginane. W literaturze z tej dziedziny zwykle nie ma mowy o konkretnych przykładach części maszyn i innych wyrobów a przedstawiane problemy są raczej abstrakcyjne. Wyróżnia się następujące podstawowe modele konstrukcji (rodzaje ustrojów):

– prętowe: pręty i wały, kratownice, cięgna, belki, ramy, pręty zakrzywione/łuki, ruszty,

– powierzchniowe: tarcze, membrany, płyty, powłoki.

Część z nich można dodatkowo podzielić na cienkościenne i grubościenne. Ustroje te mogą być poddane różnym typom obciążeń, takim jak rozciąganie/ściskanie osiowe, ścinanie, skręcanie, zginanie oraz złożone przypadki obciążeń (np. ściskanie mimośrodowe, zginanie ukośne czy zginanie ze skręcaniem).

Chcąc dokonać analitycznych obliczeń wytrzymałościowych, zwykle należy zastanowić się jaki model konstrukcji i jaki schemat obciążenia reprezentuje dany produkt. Często konieczne są uproszczenia – pomijanie pewnych elementów konstrukcji czy przyjmowanie do obliczeń podstawowego kształtu jakim można przedstawić obiekt zamiast jego faktycznej geometrii. W obliczeniach z reguły ignoruje się zaokrąglenia, niewielkie otwory itd. Również warunki podparć i obciążeń często muszą być uproszczone na potrzeby obliczeń. Należy także pamiętać o podstawowych założeniach wytrzymałości materiałów – obciążenia są statyczne a materiały traktuje się jako jednorodne, izotropowe i liniowo sprężyste. Nie uwzględnia się też nieliniowości geometrycznych wynikających z dużych odkształceń. W podejściu analitycznym z reguły pozostaje się w zakresie dziedziny wytrzymałości materiałów i jej założeń, ale zdarzają się wyjątki. Obliczenia ręczne mogą bowiem zahaczać o zaawansowaną teorię sprężystości i plastyczności czy dynamikę. Przy weryfikacji wyników analiz MES trzeba brać pod uwagę zwykle występujące różnice w założeniach modelu numerycznego i analitycznego (np. symulacje często uwzględniają nieliniowe zachowanie materiału czy nieliniowości geometryczne). Należy również zwracać uwagę na to jakie miary naprężeń i odkształceń się porównuje. W analizach MES podstawowym wynikiem są naprężenia zredukowane von Mises, które w obliczeniach analitycznych należy uzyskać z odpowiedniego wzoru wynikającego z hipotezy Huber’a-Mises’a-Hencky’ego. W programach dostępne są też poszczególne składowe tensora naprężeń i odkształceń, które często można porównać bezpośrednio z obliczeniami analitycznymi (np. naprężeniami stycznymi uzyskanymi z obliczeń na skręcanie).

Literatura

Kluczową kwestią w przypadku analitycznych obliczeń wytrzymałościowych jest dobór odpowiedniej literatury, w której można znaleźć ogólne informacje o danym zagadnieniu wytrzymałościowym, wzory i ich wyprowadzenia oraz przykładowe rozwiązania. Standardowe podręczniki do wytrzymałości, których jest wiele, stanowią cenne źródło wyżej wymienionych informacji, ale istnieją również specjalne publikacje zawierające tabele ze wzorami dla wybranych przypadków wytrzymałościowych. Najlepiej wyposażyć się w kilka książek tego typu, ale szczególnie godne polecenia jest „Roark’s Formulas for Stress and Strain” autorstwa R.G. Budynas’a i A.M. Sadegh’a. Zawiera najwięcej przypadków z różnych dziedzin i jest wręcz uznawane za pozycję obowiązkową dla inżynierów zajmujących się obliczeniami wytrzymałościowymi. W najnowszej, dziewiątej edycji tego podręcznika znajdują się rozdziały poświęcone następującym typom zagadnień:

– rozciąganie, ściskanie i ścinanie,

– belki zginane,

– pręty zakrzywione,

– skręcanie,

– płyty,

– kolumny ściskane,

– powłoki obrotowe, zbiorniki ciśnieniowe, rury,

– zagadnienia kontaktowe,

– stateczność sprężysta,

– obciążenia dynamiczne i naprężenia cieplne,

– koncentracje naprężeń,

– zmęczenie i pękanie,

– połączenia i koła zębate,

– materiały kompozytowe.

Nie zawsze jednak udaje się znaleźć w tym podręczniku interesujący nas przypadek. Wtedy można sięgnąć po odniesienia do literatury podane w każdym rozdziale tej książki lub skorzystać z innego podręcznika. Szczególnie pomocny może być jej polski odpowiednik zatytułowany „Wzory, wykresy i tablice wytrzymałościowe” autorstwa M.E. Niezgodzińskiego i T. Niezgodzińskiego. Podobna jest też książka „Formulas for Stress, Strain, and Structural Matrices” W.D. Pilkey. Istnieją również anglojęzyczne książki zawierające liczne tabele, ale bardziej wyspecjalizowane w konkretnych zagadnieniach:

– dynamika: „Formulas for Natural Frequency and Mode Shape” R.D. Blevins, „Formulas for Dynamics, Acoustics and Vibration” R.D. Blevins, „Formulas for Mechanical and Structural Shock and Impact” G. Szuladziński,

– koncentracje naprężeń: „Peterson’s Stress Concentration Factors” W.D. Pilkey, D.F. Pilkey.

Wiele wartościowych przypadków można też znaleźć w uznawanych za klasykę podręcznikach S. Timoshenko – w polskich wersjach: „Teoria płyt i powłok”, „Teoria stateczności sprężystej” oraz „Teoria sprężystości”.

W niektórych przypadkach (szczególnie tych zahaczających o zaawansowane zagadnienia) jednak tablice ze wzorami okazują się niewystarczające i należy sięgnąć po bardziej standardowe książki poświęcone danemu zagadnieniu, w tym zbiory zadań. Przykładowo, wartościowe przypadki uwzględniające plastyczność i pełzanie można znaleźć w podręcznikach „Sprężystość i plastyczność. Wybór zadań i przykładów” W. Krzysia i M. Życzkowskiego oraz „Teoria plastyczności i pełzania tom 1-2” J. Skrzypka. Interesujące przykłady są też często zawarte w pozycjach traktujących ogólnie o wytrzymałości materiałów, takich jak „Zbiór zadań z wytrzymałości materiałów” M. Banasiak, K. Grossman, M. Trombski, „Wytrzymałość materiałów tom 1-4” S. Wolny, A. Siemieniec czy „Mechanika materiałów i konstrukcji tom 1-2” M. Bijak-Żochowski i inni. Godne polecenia w przypadku zagadnień z wytrzymałości materiałów są również podręczniki autorstwa J. Zielnicy, A. Jakubowicza i Z. Orłosia, M.E. Niezgodzińskiego i T. Niezgodzińskiego, M.M. Bielajewa czy Z. Brzoski. Z nieco mniej standardowych zagadnień, warto wymienić „Podstawy obliczeń zmęczeniowych” S. Kocańdy i J. Szali, „Podstawy mechaniki kompozytów włóknistych” J. Germana, „Wprowadzenie do mechaniki pękania” tego samego autora, „Mechanikę polimerów w praktyce konstrukcyjnej” A.P. Wilczyńskiego, „Teorię uderzenia w dyskretnych układach mechanicznych” R. Grybosia oraz „Statykę i stateczność konstrukcji prętowych i cienkościennych” Z. Brzoski. Wydawnictwo Arkady, które opublikowało wspomniane wcześniej książki Timoshenko, wydało również wiele innych wartych uwagi tytułów o obliczeniach różnych typów konstrukcji, w tym serię z podtytułem „Obliczenia statyczne”. Książki te, napisane przez różnych autorów, traktują o obliczeniach: tarcz prostokątnych, płyt, powłok, prętów zakrzywionych, kratownic i ram. Zagadnienia takie jak konstrukcje cienkościenne, stateczność konstrukcji, zmęczenie materiałów, mechanika pękania, teoria sprężystości i plastyczności i reologia, teoria płyt i powłok (ustrojów powierzchniowych) czy termomechanika są omawiane w wielu odrębnych podręcznikach.

W przypadku rzadziej spotykanych zagadnień wytrzymałościowych mogą się też przydać artykuły i monografie naukowe, najczęściej anglojęzyczne. Warto jeszcze wspomnieć, iż oprócz książek opisujących ogólnie obliczenia wytrzymałościowe, bez odniesienia do konkretnych konstrukcji, istnieje też wiele podręczników skupiających się na danym typie maszyn i innych konstrukcji inżynierskich. Często zawierają one rozdziały dotyczące obliczeń (wytrzymałościowych lub innych) bądź nawet są im w całości poświęcone. Ze względu na mnogość dziedzin inżynierii i obszerność literatury w ich zakresie, nie sposób wymienić tu wszystkie warte uwagi pozycje tego typu. Podane zostaną więc jedynie wybrane przykłady z różnych działów:

– seria „Teoria i konstrukcja maszyn rolniczych” H. Bernacki, J. Dmitrewski, Cz. Kanafojski, T. Karwowski,

– „Podstawy konstrukcji obrabiarek” L.T. Wrotny,

– „Konstrukcja przyrządów i urządzeń precyzyjnych” J. Biedrzycki,

– „Wytrzymałość maszyn wirnikowych” J. Lipka,

– „Podstawy konstrukcji aparatury chemicznej cz. 1-2” J. Pikoń,

– „Wytrzymałość przemysłowych naczyń ciśnieniowych” Z. Klębowski,

– „Wytrzymałość konstrukcji lotniczych” I. Nowotarski,

– „Wagony kolejowe. Konstrukcja i badania” W. Gąsowski,

– „Wytrzymałość kadłuba statku w eksploatacji” W. Orszulok,

– „Samochód. Teoria, konstrukcja i obliczanie” K. Studziński,

– „Wytrzymałość ram i nadwozi pojazdów” F. Romanów.

Niezależnie od typu maszyny, niezwykle przydatne mogą być też liczne podręczniki z dziedziny podstaw konstrukcji maszyn, gdzie omawiane są m.in. obliczenia takich standardowych części maszyn jak elementy łączące (śruby, nity, wpusty itp.), spawy, wały, sprzęgła, hamulce, przekładnie różnego typu czy sprężyny. Wyróżnić tu można następujących autorów: L. Kurmaz, M. Dietrich, A. Skoć, E. Mazanek, A. Dziama. Z anglojęzycznych pozycji szczególnie warte uwagi jest „Shigley’s Mechanical Engineering Design” autorstwa R.G. Budynas’a i J.K. Nisbett’a. Oczywiście istnieje także szereg książek poświęconych obliczeniom różnych typów konstrukcji budowlanych (autorzy tacy jak W. Starosolski, J. Bródka, J. Żmuda, Sz. Pałkowski, M. Gwóźdź, A. Madaj czy W. Bogucki i M. Żyburtowicz). Podręczniki z dziedziny mechaniki budowli mogą być przydatne również w przypadku obliczeń niezwiązanych bezpośrednio z budownictwem, ponieważ opisują np. złożone obliczenia układów prętowych, zwłaszcza statycznie niewyznaczalnych.

Na koniec tego omówienia literatury warto dodać, że w przypadku wątpliwości co do poprawności wyniku obliczeń analitycznych warto sięgnąć po inną literaturę niż dotychczas używana. W książkach zdarzają się bowiem błędy, szczególnie często we wzorach.

Oprogramowanie wspomagające obliczenia analityczne

Obliczenia analityczne bywają bardzo pracochłonne i łatwo w nich o pomyłkę. Z tych względów, warto skorzystać z programów komputerowych typu CAS (Computer Algebra System). Są to środowiska wspomagające operacje matematyczne. Poza podstawowymi działaniami, pozwalają na obliczenia symboliczne, całkowanie i różniczkowanie, działania na wektorach i macierzach, wykorzystanie metod numerycznych i elementów programowania, tworzenie wykresów itd. Jedną z ich głównych zalet, poza tym, że dokonują przeliczeń za użytkownika, jest fakt, iż chcąc coś zmienić lub poprawić błąd w danych wejściowych bądź wzorach, nie trzeba wykonywać obliczeń od początku. Istnieją również darmowe środowiska tego typu, choć wybór nie jest zbyt duży. Szczególnie godne polecenia jest otwarte oprogramowanie wxMaxima, zbliżone do komercyjnego systemu Mathematica. Innym wartym uwagi rozwiązaniem jest SMath Studio, wzorowany na MathCAD. Program ten pozwala na wygodny zapis wzorów, wspiera jednostki (co znacznie zmniejsza ryzyko pomyłek, ponieważ źle zastosowane i przekształcone jednostki stanowią najczęstsze źródło błędów w obliczeniach wytrzymałościowych) i jest bardzo przydatny w przypadku wszelkich obliczeń inżynierskich, zwłaszcza w połączeniu ze środowiskiem Maxima do obliczeń symbolicznych i układów równań. Niestety od pewnego czasu wymaga on rejestracji a darmowa wersja ma pewne ograniczenia (w większości jednak mało uciążliwe).

Przykładowe obliczenia wytrzymałościowe

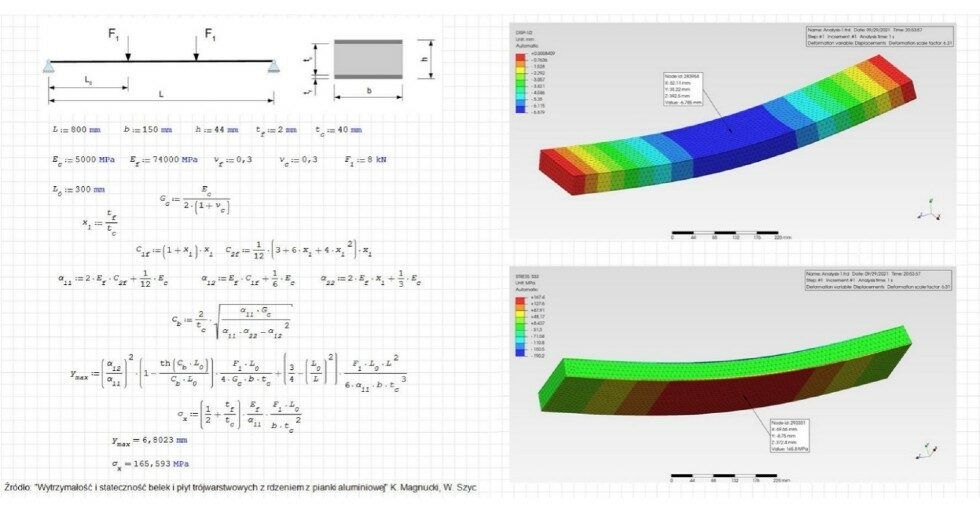
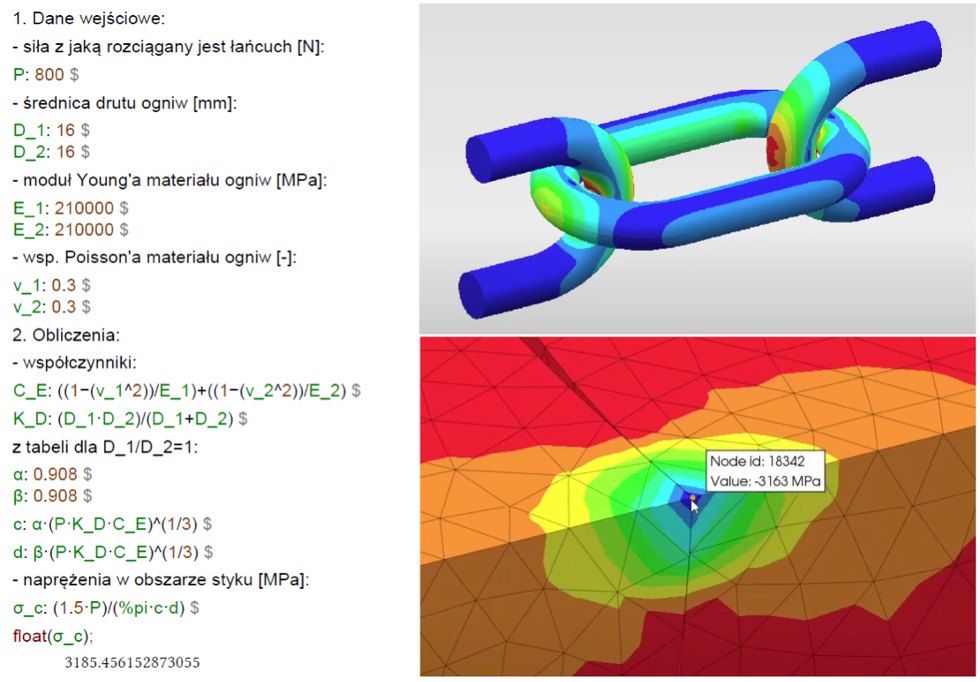
Na koniec pozostaje zaprezentować przykład obliczeń wytrzymałościowych. Rysunek na początku artykułu przedstawia obliczenia analityczne (wykonane we wspomnianym wyżej programie SMath Studio) i wyniki analizy MES (wykonanej w omawianym w poprzednich artykułach na tym portalu darmowym programie PrePoMax) na przykładzie belki trójwarstwowej. Wzory zaczerpnięte zostały z monografii prof. K. Magnuckiego „Wytrzymałość i stateczność belek i płyt trójwarstwowych z rdzeniem z pianki aluminiowej”. Z kolei przykład, który zostanie szerzej omówiony w tym akapicie to obliczenia wytrzymałościowe łańcucha ogniwowego. Co ciekawe, można w tym przypadku wykorzystać aż trzy różne podejścia do obliczeń. Przestudiowanie dostępnej literatury pozwala zauważyć, że temat ten jest rzadko poruszany z wystarczającą szczegółowością. Pierwsze ze wspomnianych podejść zostało przedstawione w książce „Dźwignice” A. Piątkiewicza i R. Sobolskiego. To opracowanie, uznawane za najlepsze w temacie dźwignic, przedstawia metodę obliczeń opartą o znane z teorii sprężystości zagadnienie Lamego. Dotyczy ono osiowosymetrycznego stanu naprężenia w płaskiej tarczy kołowej z otworem i jest wykorzystywane głównie do obliczania rur grubościennych i tarcz wirujących. Zastosowanie tego zagadnienia do obliczeń łańcuchów ogniwowych wymaga zastąpienia przekroju okrągłego prostokątnym o tym samym polu i wysokości równej średnicy drutu. Drugie podejście polega na wykorzystaniu teorii prętów silnie zakrzywionych. Jest ona często opisywana w podręcznikach z wytrzymałości materiałów, ale zwykle na innych przykładach (np. haki dźwignic). W książce „Advanced Mechanics of Materials” F.B. Seely i  J.O. Smith można znaleźć przykład jej wykorzystania do obliczeń łańcuchów. Z kolei ostatnie podejście jest oparte o zagadnienie Hertza, pozwalające wyznaczyć naprężenia kontaktowe. W literaturze można znaleźć wzory tego typu dla różnych przypadków. To podejście zostanie tu szerzej przedstawione. Odpowiednie wzory zaczerpnięte zostały z omówionej wcześniej książki „Roark’s Formulas for Stress and Strain”, chociaż można je też znaleźć m.in. we „Wzorach, wykresach i tablicach wytrzymałościowych” M.E. Niezgodzińskiego i T. Niezgodzińskiego. Styk dwóch ogniw łańcucha można uprościć do zagadnienia kontaktu dwóch walców o prostopadłych osiach i ten przypadek teorii Hertza został tu wykorzystany.

Do obliczeń analitycznych użyty został program wxMaxima. Poniższy rysunek przedstawia wydruk arkusza z tego środowiska, zestawiony z mapami konturowymi naprężeń z symulacji w PrePoMax. Analitycznie uzyskana wartość maksymalna naprężeń normalnych w miejscu styku to 3185.46 MPa, podczas gdy wartość z symulacji to 3163 MPa. Jest to bardzo dobra zgodność, biorąc pod uwagę istotę zagadnienia i stosunkowo zgrubną siatkę w modelu numerycznym.